Mathematics of Bicycle Geometry

The Mathematics of Bicycle Geometry

Preface

The following terms and definitions are my own, and some will not correspond to conventional use. In particular, I will refer to the axis of the steering tube as the "Steering Head Line" (SHL), and refer to its rake-angle as the "Steering Head Angle" (SHA). Moreover, I will use the "motorcycle" convention of measuring rake angle as a departure from the vertical, rather than from the horizontal. I find this convention more natural, as the most "naive" steering arrangement is given by SHA=0 (vertical steering tube), and it is there that the degrees of steering applied to the handlebars is exactly equal to the resulting degrees of turn evidenced in the Front Wheel Track (FWT).

The distance from the SHL to the center of the front wheel is often referred to as the "rake distance", or simply the "rake" (and sometimes, as the "offset".) I will refer to this distance as the Front Steering Radius (FSR).

Refer to the accompanying diagrams for the visual illustration of most of these terms.

Terms and Definitions

0. The Ground Plane (GP)

The horizontal plane upon which the bicycle is assumed to navigate.

1. Front Wheel Axis Line (FWA)

The line in space about which the front wheel rotates.

2. Rear Wheel Axis Line (RWA)

The line in space about which the rear wheel rotates.

3. Front Wheel Center (FWC)

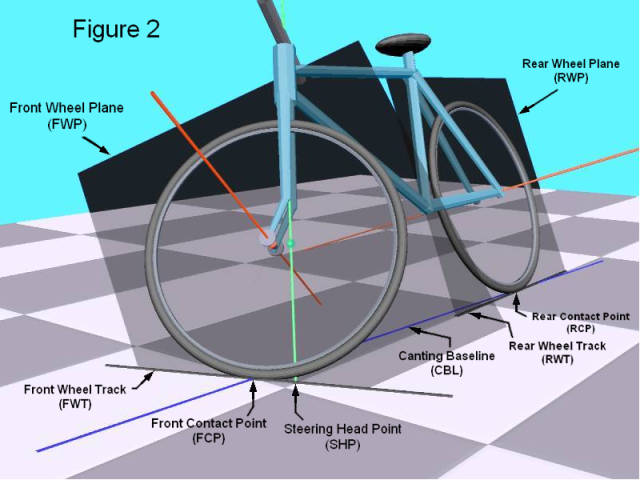
The center point of the front wheel axis.

4. Rear Wheel Center (RWC)

The center point of the rear wheel axis.

5. Front Wheel Radius (R1)

6. Rear Wheel Radius (R2)

7. Front Wheel Plane (FWP)

The plane in space defined by the orientation of the front wheel. This plane is perpendicular to the FWA and passes through the FWC.

8. Rear Wheel Plane (RWP)

The plane in space defined by the orientation of the rear wheel. This plane is perpendicular to the RWA and passes through the RWC.

9. Steering Angle (STEER)

The angle between the the FWP and the RWP (i.e., as viewed down a "steering column"). Note that this is generally NOT the degree of actual vehicle turning effected.

10. Reference Wheel Displacement (RWD)

RWD = dist(FWC,RWC) when STEER = 0.

11. Reference Wheelbase (RWB)

The horizontal component of RWD. RWB = RWD iff R1 = R2.

In general, one has RWB = sqrt( RWD^2 + (R1-R2)^2 ).

Note that during a turn, the effective wheelbase (EWB) will differ from the reference wheelbase due to the steering and the cant of the bicycle in a turn.

12. Steering Head Line (SHL)

The line in space formed by the intersection of FWP and RWP when STEER != 0.

This is the axis ordinarily associated with the steering column.

13. Steering Head Point (SHP)

Also called simply the "steering head", this is the intersection of the SHL with the GP (ground plane). Often given as a distance from the front wheel contact point (FCP), it is said to be positive steering head (or positive "castor") when located ahead of the FCP.

If the front wheel radius R1, the rake-angle SHA, and the front steering radius FSR (aka, "offset") are known, one can calculate the steering head by

SHP = (R1*sin(SHA) - FSR)/cos(SHA)

14. Steering Head Angle (SHA)

Also referred to as the "rake" of the steering, this is the angle of the SHL measured from vertical, when the RWP is held vertical. For the sake of convention, we will assign a positive SHA for "normal" slanting rake.

15. Forward Steering Radius (FSR)

The perpendicular distance between the SHL and the FWC.

Assuming that the front wheel radii R1, the steering head angle SHA, and the steering head point SHP (as measured forward of the FRONT wheel contact point) are known, the formula for calculating the front steering radius is given by

FSR = R1*sin(SHA) - SHP*cos(SHA)

16. Rearward Steering Radius (RSR)

The perpendicular distance between the SHL and the RWC.

Assuming that the rear wheel radii R2, the steering head angle SHA, and the steering head point SHP (as measured forward of the REAR wheel contact point) are known, the formula for calculating the rear steering radius is given by

RSR = SHP*cos(SHA) - R2*sin(SHA)

17. Front Contact Point (FCP)

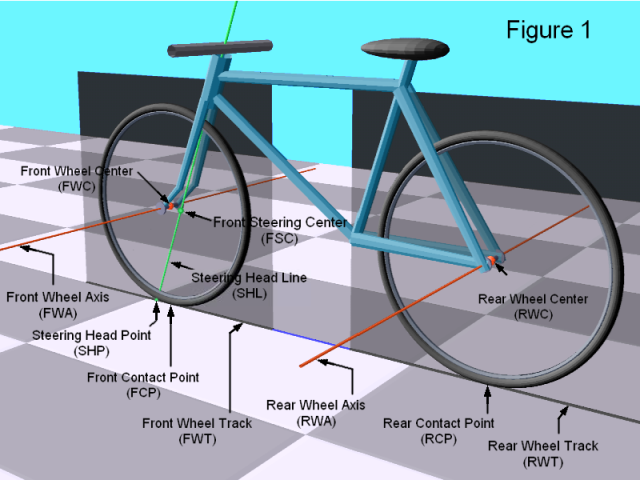
The contact point of the front wheel with the GP.

18. Rear Contact Point (RCP)

The contact point of the rear wheel with the GP.

19. Front Wheel Track (FWT)

The line in the GP formed by the SHP and FCP, or more generally, by the intersection of the Front Wheel Plane (FWP) and the Ground Plane (GP).

This line gives the "heading" of the front wheel during a turn.

20. Rear Wheel Track (RWT)

The line in the GP formed by the SHP and RCP, or more generally, by the intersection of the Rear Wheel Plane (RWP) and the Ground Plane (GP).

This line gives the "heading" of the rear wheel during a turn.

21. Turning Angle (TURN)

The (ordinarily) acute angle formed between FWT and RWT.

If the rear wheel is held vertical at a heading of 0, the TURN is equal to the relative Front Wheel Track (FWT) and is called the FWTURN, given by

FWTURN = atan( tan(STEER)*cos(SHA) )

22. Turning Center Line (TCL)

The vertical line formed by the intersection of two vertical planes, the first plane being perpendicular to the FWT and containing the FCP, the second being perpendicular to the RWT and containing the RCP.

The bicycle's various "turning radii" are essentially distances measured from the TCL.

23. Turning Radii

There are several radii that are of interest in describing the "size" of a turn. If the issue is avoiding ground objects on the outside or inside of a turn, one is interested in the Front Wheel Turning Radius (FWTR) or the Rear Wheel Turning Radius (RWTR). These are the distances from the TCL to the FCP and RCP, respectively.

As the FWTR and RWTR are typically unequal, we can define the Greater and Lesser Contact Turning Radii (GCTR and LCTR) to be the greater and lesser of FWTR and RWTR. During a constant turn, the bicycle's wheels essentially trace two circles of size FWTR and RWTR about the TCL.

As far as the dynamics of a turn are concerned, the Effective Turning Radius (ETR) must be considered. This is the distance from the TCL to the bicycle's (and rider's) center of gravity. Since a bicycle must be canted inward to a turn to maintain balance, the ETR is always less than the GCTR, and is typically less than the LCTR.

24. Canting Baseline (CBL)

The Canting Baseline is the line containing both the FCP and RCP. When canting the bicycle into a turn, the bicycle is essentially rotating with respect to the GP about the canting baseline. The "centrifugal force" created in a turn, on the bicycle's center of gravity, must be sufficient to hold the bike at a constant angle to the ground, in terms of rotation about the canting baseline.

25. Front Wheel Cant (FWCANT)

With the steering head line (SHL) held in a vertical plane (i.e., the bicycle itself is NOT canted), the FWCANT is the angle of departure of the front wheel plane (FWP) from vertical, as steering is applied.

FWCANT = asin( sin(STEER)*sin(SHA) )

26. Canting Angle

During a constant, balanced turn at constant speed, imagine a plumb-bob hanging from a line tied to the bicycle's center of gravity. That plumb-bob will point exactly to the canting baseline, and the angle it makes from the vertical is the canting angle.

27. Steering Wheelbase (SWB)

The distance between the contact points of the front and rear wheels with the ground, depending upon the degree of steering angle, while the bike is held vertical (cant=0). This distance is a function of the steering angle SHA, the FSR the RSR, and the front and rear wheel radii.

28. Effective Wheelbase (EWB)

The distance between the contact points of the front and rear wheels with the ground, when both steering and canting is considered.

29. Steering Lift (STLIFT)

Steering Lift is a measure of the degree to which a bicycle's center of gravity rises (or falls) as steering is increased. Positive steering lift causes the bike to slightly "resist steering" (tend to straighten under vertical load) and means that the rider must exert predictably positive force in order increase the steering angle. The property of positive steering lift results from a combination of factors, primarily the Forward Steering Radius (FSR) and the Steering Head Angle (SHA), but are also affected by the wheel diameters and the effective wheelbase.

In general, steering lift should be kept close to neutral if measured while the bike is held vertical, and rise only slowly as large steering angles are applied. Excessive steering lift will make the bike difficult to turn.

Nominally, one can ignore rear wheel radius and wheelbase, and take the steering lift to be proportional to the rise (or fall) of the Front Steering Center (FSC) as steering is applied, while the rear wheel is kept vertical. The following formula (derived further below) expresses steering lift in terms of front wheel radius R1, front steering radius FSR, rake angle SHA, and the amount of STEER applied:

STLIFT = R1*cos( asin( sin(STEER)*sin(SHA) ) + FSR*sin(SHA)*(1 - cos(STEER))

Note that STLIFT is comprised of two terms: The first term gives the amount by which the front wheel center drops toward the ground during steer, due to the canting of the front wheel (in turn, due to the rake angle). In the absence of steering offset (FSR = 0) the front of the bicycle frame would drop in proportion. The second term expresses the degree to which the front steering center rises with respect to the front wheel center, due to the amount of steering offset present.

Derivations

(forthcoming - please be patient)