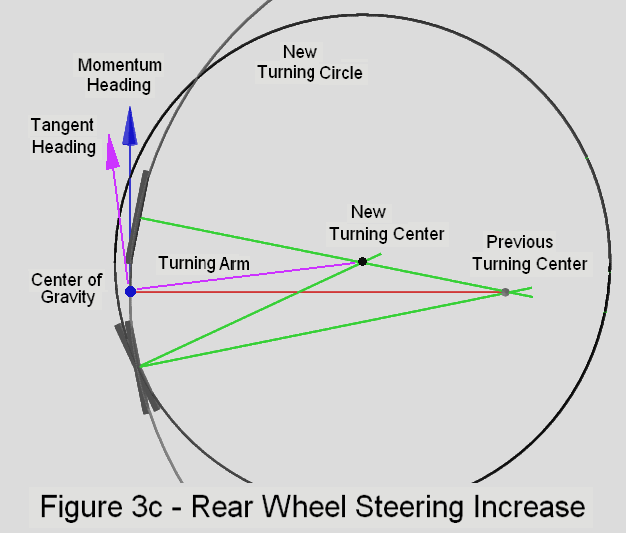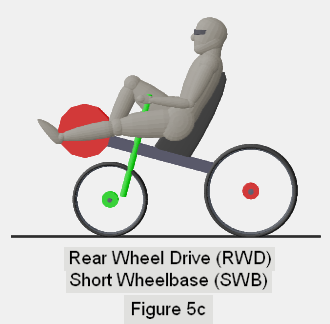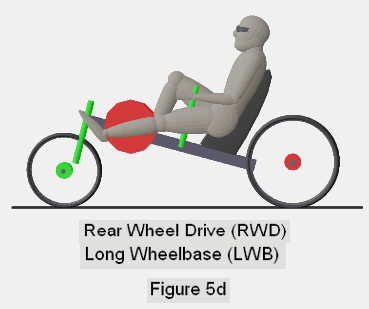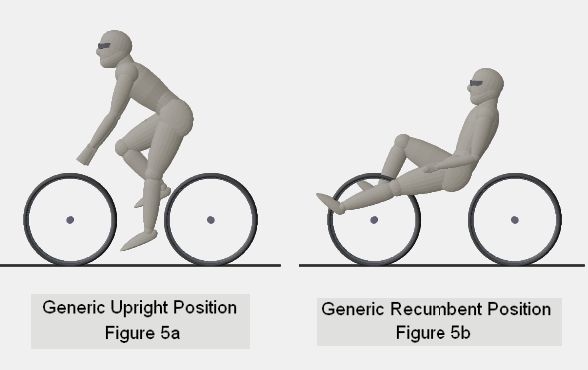
Refer to figure 5 to compare the general orientation of the rider, in the upright
versus recumbent positions. Each position has positive and negative attributes,
independent of the particular bike being ridden. Let us consider some of these:
Here, the recumbent generally provides better aerodynamics, as there is less
frontal area exposed. To approach a similar degree of aerodynamic in an upright,
the rider must double over into the "racing position", which requires the rider to
carry their upper weight on doubled-up arms, and to crane their neck backwards
in order to see forward.
B - Rider-Assisted Balance
Almost anyone can balance a 6-foot broom-handle upright on the tip of a finger.
Try to do the same thing with a 6-inch pencil, and you can appreciate why
"tallness is good" when it comes to maintaining balance. The upright rider can
adjust their weight and position easily to control the bicycle in motion.
This is more difficult for the recumbent rider, especially with recumbents
that seem to strive for the "limits of lowness" in rider position. For this reason,
having good "inherent balance" in a bicycle's geometry could be said to be
more important for a recumbent than for an upright bicycle.
In the upright position, the legs receive superior blood-flow, and one can argue
that humans have evolved to conduct most all of their heavy exertion in the upright
position (with certain horizontal exceptions ... ). Some recumbent riders complain
of numbness in their feet or toes after a long ride. For this reason, a "good"
recumbent would sacrifice some of that horizontal streamlining for a slightly
rider-canted position (pedal crank lower than the rider's seat). Of course,
the head and torso receive better blood-flow in a recumbent position.
D - Rider-Assisted Suspension
When encountering a patch of rocky roadway, the (alert) upright rider can
lift themselves off the seat, and use their legs as shock absorbers, lessening
impact upon the body (and lessening the chance of wheel damage).
In contrast, the recumbent bicycle must carry the rider's full weight at all times.
This makes full-suspension more a necessity than a luxury for the recumbent,
adding weight to the frame.
The well-designed recumbent is the clear winner here, as one of the main
motivations for recumbent bicycles is to provide the casual rider with a more
comfortable riding experience. Even the best upright touring bike requires
that the rider's upper body be canted a bit forward, and support a bit of
this upper-body weight on the arms. This can become tiring on long outings,
and the forward cant of the upper body means that the neck must continuously
lift the head up and backwards to look forward at a natural angle. The recumbent
addresses all of these issues well, but at the price of a (typically) heavier bicycle,
requiring full suspension and a larger seat to support the upper back.
Arguably, a recumbent designed for speed can exceed the speeds achievable
from an upright bicycle. With a recumbent, the full force of a rider's legs can
be applied between the pedals and the back of the rider's seat, and most people
can "leg press" far more than their own weight. It is said that an upright rider
can only exert pedal force equal to their own weight. While this is not entirely
true (the rider can "lift upward" on the handle bars while pressing down with
the legs) this can quickly become an exhausting proposition, and can interfere
with steering control. However, the salient question here is whether one can
obtain speed from a "casual" touring recumbent, comparable to that of a similar
upright. I think the answer is a qualified "yes", depending upon the specifics
of the recumbent design.
There is little that can be done for the upright bicycle that would serve to mitigate
its shortcomings. It can be argued that the recumbent position has as many,
or more shortcomings, overall. However, recumbent designs allow for greater
flexibility that can serve to mitigate most of these issues. Consider figure 5b,
where I have intentionally drawn an ambiguous (almost impossible) recumbent
position - the pedal crank would have to pass through the front wheel.
Having to "design around" this particular difficulty is responsible for much of
the variety one sees in recumbent designs. As we shall see, these design
"solutions" often lead to their own unique drawbacks, and further unique solutions.
Terminology
Recumbent bicycle designs can be divided several ways, the most common being
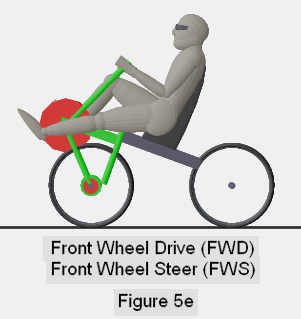
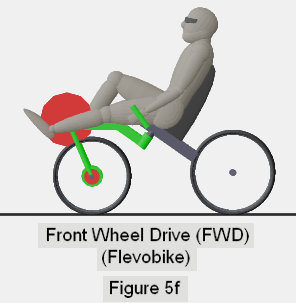
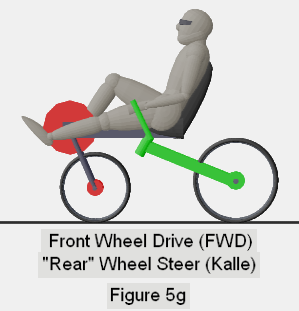
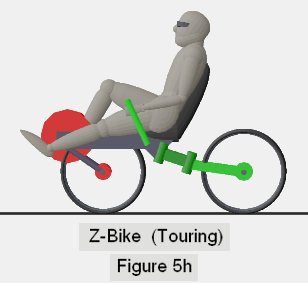
- RWD versus FWD (Rear Wheel Drive versus Front Wheel Drive)
- LWB versus SWB (Long Wheelbase versus Short Wheelbase)
and to a less common extent
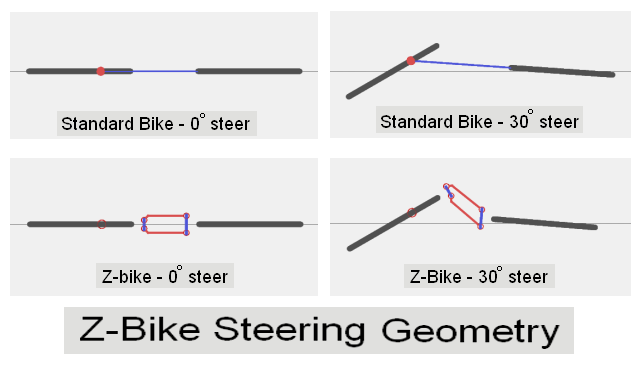
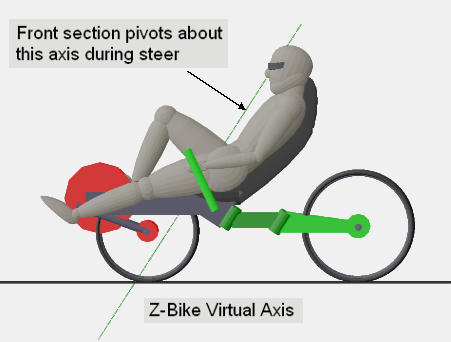
- FWS versus RWS (Front Wheel Steer versus Rear Wheel Steer)
Below, I depict (figuratively) each of these designs (or their most common
implementations) and discuss what I feel are the gains and losses associated
with each. I begin with the Rear Wheel Drive designs, then move on to
Front Wheel Drive and then "Rear Wheel Steer", as this order provides a
nice sequence of problem-solution-problem motivated alterations.
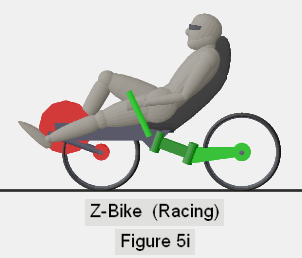
With each figure, I use red disks to indicate the "powered" wheel, and
the travel of the feet around the pedal crank. I use a green disk to identify
the wheel that steers, and green for any major frame components that move
together with the wheel during a steer. The remainder of the frame is
depicted in dark gray.